发表更新计算机基础 / 数据结构与算法22 分钟读完 (大约3256个字)

数据结构与算法(三)：树 和 二叉树

有些数据的逻辑关系并不是简单的线性关系，常常存在一对多，甚至多对多的情况。例如，一个家族的 “家谱”，企业的职级关系等、书本的目录章节等都可以用树型数据结构来描述。

树 和 图 是典型的非线性数据结构。本篇描述对 树 和 二叉树 的理解。

树

定义

树（tree）是一种数据结构，由是 n（n>=0） 个节点的组成一个有层次关系的有限集合。之所有称之为树，是因为其看起来像一棵倒持的树，，也就是说它是根朝上，叶子朝下的。

当 n = 0 时，称为空树。在任意一个非空树中，有如下特点：

  1. 有且只有一个特定的节点被称为根结点（root）。
  2. 当 n > 1 时，其余节点可分为 m（m > 0）个互不相交的有限集，每一个集合本身又是一棵树，并称为根的子树（subtree）。
  3. 父节点：上级节点称为父节点。
  4. 孩子节点： 延伸出来的下级节点称为孩子节点。
  5. 叶子节点： 末端节点，没有延伸出子节点。
  6. 兄弟节点：同级，由同一个父节点衍生出来的节点。
  7. 树的深度：树的最大层级数，也称为树的高度。

种类

  • 无序树：树中任意节点的子节点之间没有顺序关系。也称为自由树。
  • 有序树：树中任意节点的子结点之间有顺序关系。
  • 二叉树：每个节点最多含有两个子树（子节点）。
    • 满二叉树：所有非叶子节点都存在左右叶子节点，并且所有叶子节点都在同一层级。
    • 完全二叉树：
    • 霍夫曼树：带权路径最短的二叉树，又称为最优二叉树。
    • 红黑树：一种自平衡二叉查找树。
  • B 树：
  • B+ 树：

二叉树

定义

二叉树（binary tree）的二叉指这种树的每个节最多有 2 个子节点。也可能只有 1 个子节点，或没有子节点。

二叉树的 2 个子节点，一个称为左孩子节点（left child），一个被称为右孩子节点（right child），这两个子节点的顺序是固定的。

二叉树还有两种特殊形式，一个叫作 满二叉树，另一个叫作 完全二叉树。

满二叉树

满二叉树：一个二叉树的所有非叶子节点都存在左右叶子节点，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。

满二叉树的每一个分支都是满的。

完全二叉树

完全二叉树：完全二叉树是由满二叉树而引出来的。对一个有 n 个节点的二叉树，按层级顺序编号，则所有节点的编号为从 1 到 n。如果这个树所有节点和同样深度的满二叉树的编号为从 1 到 n 的节点位置相同，则这个二叉树为完全二叉树。

又解：对于深度为 K 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的节点一 一对应时称之为完全二叉树。

如下示意图，完全二叉树与满二叉树深度相同，节点顺序编号相同，最后一个节点及之前的所有节点与满二叉树节点相同。

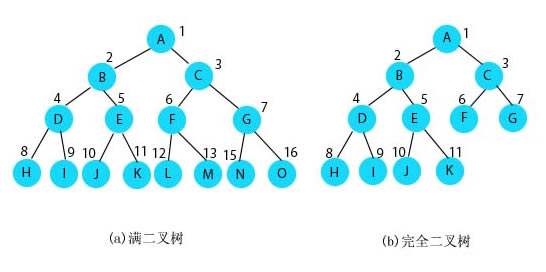
满二叉树与完全二叉树

完全二叉树没有满二叉树那么苛刻，满二叉树要求所有分支都是满的，完全二叉树只需要保证最后一个节点之前的节点都齐全即可。

二叉树物理存储结构

链式存储结构

链式存储是二叉树最直观的存储方式。链式结构的二叉树的每一个节点包含 3 部分：

  • 存储数据的 data 变量。
  • 指向左节点的 left 指针。
  • 指向右节点的 right 指针。

数组存储结构

使用数组存储时，是按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左节点或右节点空缺，则该数组的相应位置也空出来。这样方便定位二叉树的子节点和父节点。

假设一个父节点的下标是 parent，那么它的左节点下标 left = 2 * parent + 1；右孩子节点下标 right = 2 * parent + 2。

反过来，假设左节点的下标是 left，那么它的父节点的下标 parent = (left - 1) / 2。

对于一个稀疏的二叉树来说，用数组来存储是非常浪费空间的。另一种特殊的完全二叉树-二叉堆是用数组存储的。

二叉树的应用

二叉树包含许多特殊的形式，每种形式都有自己的作用，但主要的应用还是进行 查找操作 和 维持相对顺序 这两个方面。

二叉查找树

  1. 查找

    二叉树的树形结构很适合应用于索引的场景。

    二叉查找树（binary search tree）：对称 二叉排序树（Binary Sort Tree），主要作用是进行查找操作。在二叉树的基础上增加了以下几个条件。

    • 如果左子树不为空，则左子树上的所有节点的值均小于根节点的值。
    • 如果右子树不为空，则右子树上的所有节点的值均大于根节点的值。
    • 左、右子树也都是二叉查找树。

    这些条件保证了二叉树的有序性，非常放便用于查找。

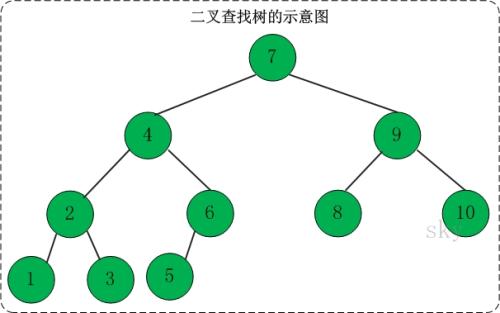
    二叉查找树

    对于一个 节点分布相对均衡 的二叉查找树来说，如果节点总数是 n，那么搜索节点的时间复杂度就是 Ο(logn)，和树的深度是一样的。

    这种依靠比较大小来逐步查找的方式，和二分查找算法非常相似。

  2. 维持相对顺序

    二叉查找树又称为二叉排序树，新插入的节点同样要遵循二叉排序树的原则。

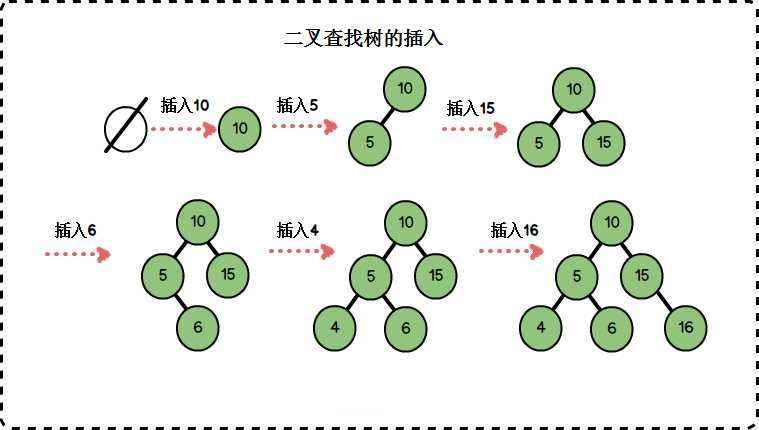
    二叉查找树的插入演示

    见上图的插入演示，在节点分布相对均衡的情况下，维持了相对的顺序。

    二叉查找树可能存在另一个问题，当大量的节点分布非常不均衡的情况下，会存在一边节点非常长的怪异情况。二叉查找树的几种形态见下图：

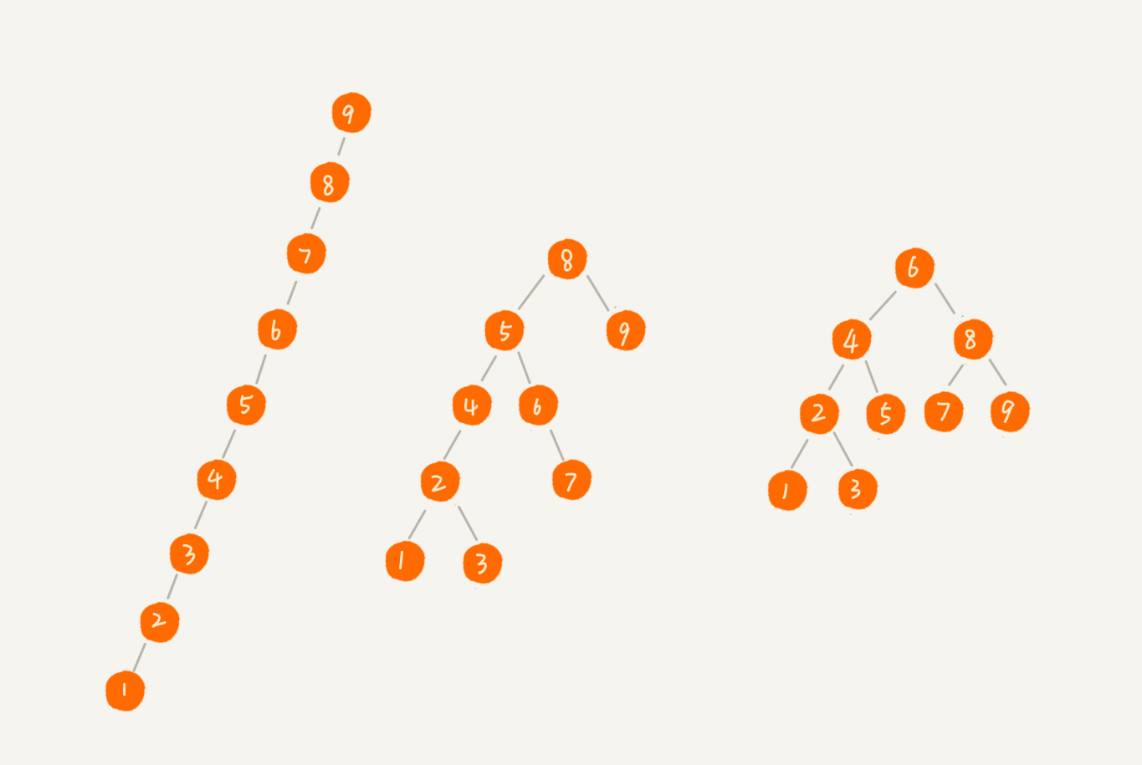
    二叉查找树的形态

    要解决一边节点过长的情况，就涉及到了二叉树的自平衡 了。二叉树自平衡的方式有多种，如 红黑权、AVL 树、树堆 等。

    除了二叉树维持相对顺序外， 二叉堆 也维持着相对顺序，并且条件要宽松些，只要求父节点比左右子节点都大。

二叉树的遍历

在计算机中，遍历本身是一个线性操作。所以遍历同样具有线结构的数组或链表就非常简单容易。

而二叉树是典型的非线性数据结构，遍历时需要把非线性关联节点转换为一个线性的序列。以不同的方式遍历，遍历出的序列顺序也不同。

从更宏观的角度来看，数据结构与算法的遍历归为两大类：深度优先遍历 和 广度优先遍历。深度优先 和 广度优化这两个概念不止局限于二叉树，它们更是一种抽象的算法思想，决定访问某些复杂数据结构的顺序。

  • 深度优先遍历（前序遍历，中序遍历，后序遍历）。

    偏向于纵深，“一头扎到底” 的访问方式。

  • 广度优先遍历（层序遍历）

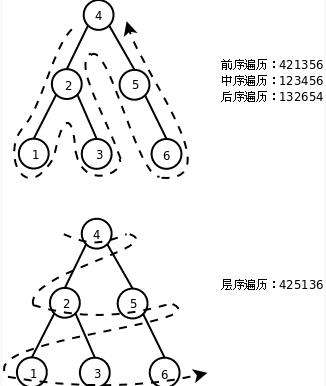
前序遍历

前顺遍历的输出顺序是：根节点，再访问左子树，再访问右子树。

  1. 先输出根节点。
  2. 从上往下输出左子树的左节点，再输出右节点。
  3. 再输出根节点的右子树的左节点，再输出右节点。

中序遍历

中序遍历的输出顺序是：左子树、根节点、右子树。

  1. 先访问根节点的左子节点，如果左子节点是子树，则继承深入访问，直到没有下级节点，并输出该节点（叶子节点）。
  2. 向上输出父节点，再输出父节点的右子节点，也遵循第 1 条规则。
  3. 右子树输出完后后，再输出整个二叉树的根节点。
  4. 再输出根节点的右子节点，也遵循第 1 条规则。

后序遍历

后序遍历的输出顺序是：左子树、右子树、根节点。

  1. 先输出左子节点的所有叶子节点，再输出父节点。
  2. 再输出右子树的所有叶子节点，再输出父节点。
  3. 最后输出根节点。

层序遍历

按照从根节点到叶子节点的层级关系，一层一层横向遍历各个节点。要实现层序遍历，需要借助 队列 辅助工作。

从根节点开始，将元素存入队列执行入队和出队操作，先左树节点，再右树节点。

遍历实现逻辑

  1. 递归实现遍历

    用递归方式实现前序、中序、后序遍历，是最简单的方式。区分仅在于输出的执行位置不同，前序遍历输出在前，中序遍历输出在中间，后序遍历输出在最后。

  2. 借助栈实现遍历

    还可以用 栈 来实现二叉树的遍历，栈 与 递归一样也具有回溯的特性。

    通过出栈入栈的方式实现遍历，子节点入栈，父节点出栈。

遍历顺序图

遍历代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

/**
 * 创建二叉树并遍历
 */
public class BinaryTree {

    /**
     * 构建二叉树
     *
     * @param inputList 输入序列
     * @return
     */
    public static TreeNode createBinaryTree(LinkedList<Integer> inputList) {
        TreeNode node = null;
        if (inputList == null || inputList.isEmpty()) {
            return null;
        }
        Integer data = inputList.removeFirst();
        if (data != null) {
            node = new TreeNode(data);
            //先创建左节点，直到为 null,再创建右边节点
            node.leftChild = createBinaryTree(inputList);
            node.rightChild = createBinaryTree(inputList);
        }
        return node;
    }

    /**
     * 递归实现：前序遍历
     *
     * @param node
     */
    public static void preOrder(TreeNode node) {
        if (node == null) {
            return;
        }

        System.out.println(node.data);
        //递归调用输出左树节点直到 null, 再输出右树节点
        preOrder(node.leftChild);
        preOrder(node.rightChild);
    }

    /**
     * 非递归实现：前序遍历
     *
     * @param treeNode
     */
    public static void preOrderWithStack(TreeNode treeNode) {
        Stack<TreeNode> stack = new Stack<>();

        while (treeNode != null || !stack.isEmpty()) {
            //迭代访问节点的左子节点，并入栈
            while (treeNode != null) {
                System.out.println(treeNode.data);
                stack.push(treeNode);
                treeNode = treeNode.leftChild;
            }

            //如果节点没有左子节点，则弹出栈顶节点，访问右子节点
            if (!stack.isEmpty()) {
                treeNode = stack.pop();
                treeNode = treeNode.rightChild;
            }
        }

    }

    /**
     * 递归实现：中序遍历
     *
     * @param node
     */
    public static void middleOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        //递归调用直到下级为 null, 再输出叶子节点
        middleOrder(node.leftChild);
        System.out.println(node.data);
        middleOrder(node.rightChild);
    }

    /**
     * 递归实现：后序遍历
     *
     * @param node
     */
    public static void postOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        postOrder(node.leftChild);
        postOrder(node.rightChild);
        System.out.println(node.data);

    }

    /**
     * 递归实现：层序遍历
     *
     * @param root
     */
    public static void levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.println(node.data);
            if (node.leftChild != null) {
                queue.offer(node.leftChild);
            }
            if (node.rightChild != null) {
                queue.offer(node.rightChild);
            }
        }
    }

    public static void main(String[] args) {
        Integer[] intArray = {6, 2, 4, null, null, 3, null, null, 5, null, 8};
        LinkedList<Integer> inputList = new LinkedList<>(Arrays.asList(intArray));

        TreeNode node = BinaryTree.createBinaryTree(inputList);
        System.out.println(node);

        System.out.println("--------前序--------");
        preOrder(node);//6,2,4,3,5,8
        System.out.println("--------中序--------");
        middleOrder(node);//4,2,3,6,5,8
        System.out.println("--------后序--------");
        postOrder(node);//4,3,2,8,5,6
        System.out.println("--------层序--------");
        levelOrder(node);//6,2,5,4,3,8
        System.out.println("----非递归实现前序遍历--------");
        preOrderWithStack(node);//6,2,4,3,5,8

    }
}

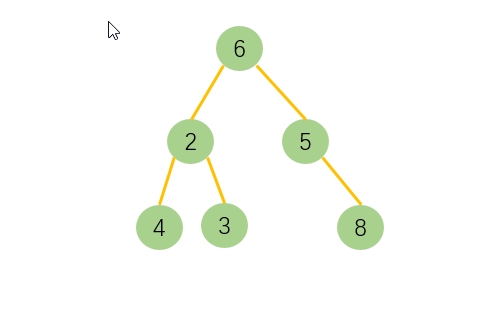
上面代码创建的二叉树结构如下图：

代码中创建的二叉树

数据结构与算法(三)：树 和 二叉树

http://blog.gxitsky.com/2019/07/19/DataStructure-03-tree-binarytree/

作者

光星

发布于

2019-07-19

更新于

2022-06-17

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我
×