发表更新计算机基础 / 数据结构与算法32 分钟读完 (大约4773个字)

数据结构与算法(五)：FIFO, LRU, LFU 缓存淘汰算法

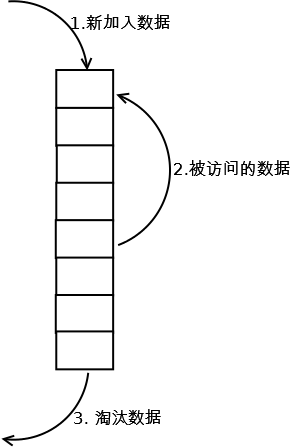
服务器内存有限，不可能持续地往内存中存入数据，就需要对内存中的数据进行淘汰处理，通过制定淘汰策略（算法）以保证内存持续可用，使内存中的数据价值最大化。

应用层的缓存淘汰算法基本都是借用操作系统的内存管理算法，以称为内存页置换算法。

内存页置换算法

常见的内存页置换算法有以下几种：

算法 中文 注释
Optimal算法 最优算法 一种理论上的算法，无法实现，可作为其他算法性能的参照标准
FIFO算法 先时先出算法 First-In First-Out，实现简单，效率低
可能会淘汰频繁访问的页面
Second Chance算法 第二次机会算法 基本思想是与FIFO相同的，但是有所改进。
Clock算法 时钟算法 是对第二次算法的改进，一种现实可行的算法
有简单的Clock置换算法，改进型Clock置换算法
LRU算法 最近最旧未使用算法 Least Recent Used，基于时间维度
使用时间戳标记，遍历逐出最早的数据；
或按最近访问排序，最近访问在队头，逐出队尾
LFU算法 最近最少使用算法 Least Frequently Used，基于次数维度
使用记数器，按次数排序或遍历，逐出次数最小的数据
PBA算法 页面缓冲算法 Page Buffering Algorithm，降低了页面换进、换出的频率
使磁盘I/O的操作次数大大减少

FIFO-先进先出

FIFO（First In First Out）：先进先出，先进入的缓存数据先淘汰，使用队列来实现。核心思想是假定刚刚加入的数据总会被访问到。

FIFO 是典型的队列数据结构的特点，队头弹出，队尾插入。

特点：命中率低，复杂度相对比较简单，存储成本地，速度快，但使用价值不高，缓存设计不可能把不是本次想要的数据都从队头弹出。

Mybatis 的 FIFO 缓存策略（FifoCache）就是基于双端队列（Deque，底层是链表 LinkedList）实现的。

数组队列实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
/**
 * @author gxing
 * @desc
 * @date 2021/1/21
 */
public class ArrayQueue {
    /**
     * 最大容量
     */
    private int maxSize;
    /**
     * 数组
     */
    private Object[] array;
    /**
     * 头标记
     */
    private int front;
    /**
     * 尾索引
     */
    private int rear;

    //构建函数
    public ArrayQueue(int maxSize) {
        this.maxSize = maxSize;
        array = new Object[this.maxSize];
        front = -1;
        rear = -1;
    }

    /**
     * 判空
     *
     * @return
     */
    public boolean isEmpty() {
        return front == rear;
    }

    /**
     * 判满
     *
     * @return
     */
    public boolean isFull() {
        return rear == maxSize - 1;
    }

    /**
     * 队尾插入
     *
     * @param e
     */
    public void add(Object e) {
        if (isFull()) {
            throw new BusinessException("the array queue is full!");
        }
        rear++;
        array[rear] = e;
    }

    /**
     * 队头弹出
     *
     * @return
     */
    public Object getHead() {
        if (isEmpty()) {
            throw new RuntimeException("the array queue is empty!");
        }
        Object result = array[0];
        // 弹出头,后面元素全部前移
//        System.arraycopy(array, 1, array, 0, array.length - 1);
        for (int i = 0; i < array.length - 1; i++) {
            array[i] = array[i + 1];
        }
        // 最后元素置空
        array[rear] = null;
        // 最后元素索引前移一位
        rear--;
        return result;
    }
}

LRU-最近最久未使用

LRU（Least Recently User）：最近最旧未使用（基于时间维度），是一种常用的页面置换算法，选择最近最少使用的页面予以淘汰。
该算法赋予每个页面一个访问字段，用来记录一个页面自上次被访问以来所经历的时间 t，当须淘汰一个页面时，选择现有页面中其 t 值最大的，即最近最少使用的页面予以淘汰。

LRU 的核心思想：如果数据最近被访问过，那么将来被访问的几率也更高。

总体思路：

  • 一种是添加被访问时的时间标记，以此时间排序或遍历所有，值越小表示越早，在删除操作时移除此元素。
  • 采用链表来实现，新数据插入到链表头，被访问的移到链表头，在删除操作时删除链表尾。

单向链表实现

实现逻辑

  • 插入：每次插入新数据时，将新数据插入到链表的头部
  • 访问：每次将被访问（命中）的数据移到链表头部
  • 移除：当链表满时，就将链表尾部的数据丢弃

链表实现LRU

优缺点

  • 优点：非常适合热点数据，命中率高；插入数据快（总是插入到头），复杂度O(1)。
  • 缺点：查询和删除慢慢（复杂度为 O(n)），需要遍历链表。
  • 链表实现是将新数据插入到链表头，假如其数据大小接近缓存容量且是周期性数据，则会污染缓存（独占缓存，将有效缓存数据全部挤出）。

Java实现

节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 单向链表节点
 */
public class Node<T> {

    String key;
    T value;
    Node<T> next;

    public Node(String key, T value) {
        this.key = key;
        this.value = value;
    }
}

单向链表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
/**
 * @desc 单向链表缓存
 * @date 2021/1/19
 */
public class LinkedListCache<T> {
    // 缓存大小,默认为8
    private int capacity = 8;
    // 链表长度
    private int size;

    // 头
    private Node<T> head;
    // 尾
    private Node<T> last;

    public LinkListCache() {
    }

    public LinkListCache(int capacity) {
        this.capacity = capacity;
    }

    /**
     * 插入
     * 最近使用插入到链表头
     *
     * @param key
     * @param value
     */
    public void insert(String key, T value) {
        Node<T> temp = head;
        if (size == 0) {
            // 缓存为空
            Node<T> node = new Node<>(key, value);
            head = node;
            last = node;

        } else if (size < capacity) {
            // 缓存还有空间
            head = new Node<>(key, value);
            head.next = temp;
        } else {
            // 移除链尾
            this.removeLast();
            // 插入链头
            head = new Node<>(key, value);
            head.next = temp;
        }
        size++;
    }

    /**
     * 查询
     *
     * @param key
     * @return
     */
    public T get(String key) {
        Node<T> preNode = null;
        Node<T> temp = head;
        Node<T> first = head;

        for (int i = 0; i < size; i++) {

            if (temp.key.equals(key)) {

                if (temp.equals(head)) {
                    // 链表头
                    return temp.value;
                } else if (temp.next == null) {
                    // 链表尾
                    head = temp;
                    head.next = first;
                    preNode.next = null;
                    last = preNode;
                } else {
                    // 链表中
                    Node<T> next = temp.next;
                    head = temp;
                    head.next = first;
                    preNode.next = next;
                }
                return temp.value;
            }
            preNode = temp;
            temp = temp.next;
        }
        return null;
    }


    /**
     * 删除链表尾(最近最少使用)
     */
    public void removeLast() {
        Node<T> temp = head;
        // 倒数第三个, next就是倒数第二个
        for (int i = 0; i < size - 2; i++) {
            temp = temp.next;
        }
        // 倒数第二个置为队尾, next置空
        temp.next = null;
        last = temp;
        size--;
    }
}

哈希+单向链表实现

实现逻辑

哈希 + 链表的实现逻辑：用哈希表来存储数据，用链表来记录最近使用的数据。

  • 插入：每次插入时，判断 Hash 表中是否存在，不存在则直接存入Hash表并插入到链表头中；
    如果存在，则查询链表并将其移到链表头中。
  • 访问：判断 Hash 表中是否存在，存在则取出值（节点），并将该节点移到链表头，返回值。
  • 移除：当链表满时，就将丢弃链表尾的数据。

优缺点

  • 优点：非常适合热点数据，命中率高；插入数据快（总是插入到头），复杂度O(1)；查询快，直接从 Hash 表中取值。
  • 缺点：查询和删除慢，因为还要操作链表，Hash表的查询优势就体现不出来，要到单向链表中查询和删除，还是需要遍历链表。
    该缺点可以通过双向链表来优化。双向链表的删除就不需要遍历链表。

Java实现

节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 单向链表节点
 */
public class Node<T> {

    String key;
    T value;
    Node<T> next;

    public Node(String key, T value) {
        this.key = key;
        this.value = value;
    }
}

单向链表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
/**
 * @desc 单向链表
 * @date 2021/1/19
 */
public class LinkedList<T> {
    // 头
    private Node<T> head;
    // 尾
    private Node<T> last;

    /**
     * 插到链表头
     *
     * @param node
     */
    public void addToHead(Node<T> node) {
        if (head == null) {
            head = node;
            last = node;
        } else {
            Node<T> temp = head;
            head = node;
            head.next = temp;
        }
    }

    /**
     * 移到链表头
     *
     * @param node
     */
    public void moveToHead(Node<T> node) {
        Node<T> preNode = null;
        Node<T> temp = head;
        Node<T> first = head;

        for (; ; ) {
            // 遍历查找
            if (temp.equals(node)) {

                if (temp.equals(head)) {
                    // 头
                    break;
                } else if (temp.next == null) {
                    // 链表尾
                    head = temp;
                    head.next = first;
                    preNode.next = null;
                    last = preNode;
                    break;
                } else {
                    // 链表中
                    Node<T> next = temp.next;
                    head = temp;
                    head.next = first;
                    preNode.next = next;
                    break;
                }
            }
            preNode = temp;
            temp = temp.next;

            if (temp == null) {
                break;
            }
        }

    }


    /**
     * 删除链表尾(最近最少使用)
     */
    public void removeLast() {
        if (last == null) {
            return;
        }

        if (head == last) {
            head = null;
            last = null;
            return;
        }

        Node<T> temp = head;
        Node<T> preNode = head;
        // 倒数第三个, next就是倒数第二个
        for (; ; ) {
            if (temp.next == null) {
                last = preNode;
                preNode.next = null;
                break;
            }
            preNode = temp;
            temp = temp.next;
        }
    }
}


缓存实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/**
 * @desc 哈希表+链表
 * @date 2021/1/20
 */
public class HashLinkedListCache<T> {
    /**
     * 最大容量
     */
    private int capacity = 8;

    HashMap<String, Node<T>> map;
    LinkedList<T> list;

    public HashLinkedListCache() {
        this.list = new LinkedList<>();
        this.map = new HashMap<>();
    }

    public HashLinkedListCache(int capacity) {
        this.list = new LinkedList<>();
        this.map = new HashMap<>(capacity);
        this.capacity = capacity;
    }

    /**
     * 插入
     *
     * @param key
     * @param value
     */
    public void put(String key, T value) {
        // 存在
        if (map.containsKey(key)) {
            Node<T> node = map.get(key);
            node.value = value;
            list.moveToHead(node);
        } else {
            // 不存在
            Node<T> node = new Node<>(key, value);
            if (!(map.size() < capacity)) {
                list.removeLast();
            }
            map.put(key, node);
            list.addToHead(node);
        }
    }

    /**
     * 查询
     *
     * @param key
     * @return
     */
    public T get(String key) {
        Node<T> node = map.get(key);
        if (node != null) {
            list.moveToHead(node);
            return node.value;
        }
        return null;
    }
}

哈希+双向链表实现

实现逻辑

哈希 +双向链表的实现逻辑：用哈希表来存储数据，用链表来记录最近使用的数据。是在 哈希+单向链表的基础上。
借助双向链表的特性，优化移动链表中元素到头时的操作，不用再遍历链表查询。

  • 插入：每次插入时，判断 Hash 表中是否存在，不存在则直接存入Hash表并插入到链表头中；
    如果存在，将其移到链表头中，设置前后节点的指针。
  • 访问：判断 Hash 表中是否存在，存在则取出值（节点），并将该节点移到链表头，返回值。
  • 移除：当链表满时，就将丢弃链表尾的数据。

优缺点

  • 优点：非常适合热点数据，命中率高

    插入（总是插入到头），复杂度O(1)

    查询快，直接从 Hash 表中取值

    删除快，直接删除尾节点，重置上一节点为尾节点

  • 缺点：无

Java实现

节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * 双向链表节点
 */
public class Node<T> {

    String key;
    T value;
    Node<T> preNode;
    Node<T> nextNode;

    public Node(String key, T value) {
        this.key = key;
        this.value = value;
    }
}

双向链表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
/**
 * @desc 双向链表
 * @date 2021/1/19
 */
public class DoubleLinkList<T> {
    // 头
    private Node<T> head;
    // 尾
    private Node<T> last;

    /**
     * 插到链表头
     *
     * @param node
     */
    public void addToHead(Node<T> node) {
        if (head == null) {
            head = node;
            last = node;
            last.preNode = head;
        } else {
            Node<T> temp = head;
            head = node;
            head.nextNode = temp;
            temp.preNode = head;
        }
    }

    /**
     * 移到链表头
     *
     * @param node
     */
    public void moveToHead(Node<T> node) {

        if (node.equals(head)) {
            return;
        }

        Node<T> temp = head;
        Node<T> preNode = node.preNode;
        Node<T> nextNode = node.nextNode;

        head = node;
        head.preNode = null;
        head.nextNode = temp;
        temp.preNode = head;
        preNode.nextNode = nextNode;
    }


    /**
     * 删除链表尾(最近最少使用)
     */
    public void removeLast() {
        if (last == null) {
            return;
        }

        if (head == last) {
            head = null;
            last = null;
            return;
        }
        last = last.preNode;
        last.nextNode = null;
    }
}

缓存实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/**
 * @desc 哈希表+链表
 * @date 2021/1/20
 */
public class HashLinkedListCache<T> {
    /**
     * 最大容量
     */
    private int capacity = 8;

    HashMap<String, Node<T>> map;
    DoubleLinkList<T> list;

    public HashLinkedListCache() {
        this.list = new DoubleLinkList<>();
        this.map = new HashMap<>();
    }

    public HashLinkedListCache(int capacity) {
        this.list = new DoubleLinkList<>();
        this.map = new HashMap<>(capacity);
        this.capacity = capacity;
    }

    /**
     * 插入
     *
     * @param key
     * @param value
     */
    public void put(String key, T value) {
        // 存在
        if (map.containsKey(key)) {
            Node<T> node = map.get(key);
            node.value = value;
            list.moveToHead(node);
        } else {
            // 不存在
            Node<T> node = new Node<>(key, value);
            if (!(map.size() < capacity)) {
                list.removeLast();
            }
            map.put(key, node);
            list.addToHead(node);
        }
    }

    /**
     * 查询
     *
     * @param key
     * @return
     */
    public T get(String key) {
        Node<T> node = map.get(key);
        if (node != null) {
            list.moveToHead(node);
            return node.value;
        }
        return null;
    }
}

LinkedHashMap实现

JDK 的 LinkedHashMap 继承自 HashMap，拥有 HashMap 的所有特性，同时 LinkedHashMap 给节点增加了 head 和 tail 指针，用于实现双向链表。

注意：LinkedHashMap 不是线程安全的，用作缓存的话需要加同步处理。最简单粗暴的操作是重写 HashMap 方法，所有方法上加锁。

1
2
3
4
5
6
7
8
9
/**
 * The head (eldest) of the doubly linked list.
 */
transient LinkedHashMap.Entry<K,V> head;

/**
 * The tail (youngest) of the doubly linked list.
 */
transient LinkedHashMap.Entry<K,V> tail;

最近访问排序

LinkedHashMap 默认是按插入的顺序保存数据，新的数据插入到双向链表尾部。

Mybatis 的 LRU 缓存策略（LruCache）就是基于 LinkedHashMap 实现的。

可能通过构造方法的 accessOrder 参数来控制是否开启访问排序；设置为 true 开启访问排序，则最新的数据放到双向链表尾部。

1
2
3
4
5
6
7
8
public LinkedHashMap(int initialCapacity,
                     float loadFactor,
                     boolean accessOrder) {
    super(initialCapacity, loadFactor);
    this.accessOrder = accessOrder;
}
// 使用
LinkedHashMap<String, Object> cache = new LinkedHashMap<>(6, 0.75f, true);

移除最旧元素

LinkedHashMap 提供了移除最旧元素方法，但默认是没有开启的，如果一直往 LinkedHashMap 中添加元素就会一直触发自动扩容，若启用了移除旧元素方法，map 满了就会移除旧元素，触发自动扩容则是有限的。

1
2
3
protected boolean removeEldestEntry(Map.Entry<K,V> eldest) {
    return false;
}

自定义一个 Map 继承 LinkedHashMap ，重写 removeEldestEntry 方法，示例：

1
2
3
4
5
// 维护100个元素，然后在每次添加新元素时删除最老的元素，从而保持100个元素的稳定状态。
private static final int MAX_ENTRIES = 100;
protected boolean removeEldestEntry(Map.Entry eldest) {
    return size() > MAX_ENTRIES;
}

该方法由插入新元素的 put 和 putAll 方法调用。给实现者提供了在每次添加新元素时删除最旧元素的机会， 如果将此 map 用作缓存，这非常有用：它允许 map 通过删除最旧的元素来减少内存消耗。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class LruLinkedHashMap<K, V> extends LinkedHashMap<K, V> {

    private int size;

    public LruLinkedHashMap(int initialCapacity,
                            float loadFactor,
                            boolean accessOrder) {
        super(initialCapacity, loadFactor, accessOrder);
        this.size = initialCapacity;
    }

    /**
     * 重写LinkedHashMap的removeEldestEntry方法
     * 移除最旧的元素（最近最少使用）
     *
     * @param eldest
     * @return
     */
    @Override
    protected boolean removeEldestEntry(java.util.Map.Entry<K, V> eldest) {
        if (size() > size) {
            return true;
        }
        return false;
    }
}

HashMap+LinkedList

借助 JDK 自带的 HashMap 和 LinkedList 实现。

LinkedList

LinkedList 是 List 和 Deque 接口的双向链表实现，实现了 list 所有的可选操作。

LinkedList 定义一头节点，尾节点，新增头尾节点，查询头尾节点，移除头尾节点的操作。

JDK 自带 LinkedList

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
package java.util;

import java.util.function.Consumer;

public class LinkedList<E> extends AbstractSequentialList<E> implements List<E>, Deque<E>, Cloneable, java.io.Serializable {
    transient int size = 0;

    /**
     * 头节点
     */
    transient Node<E> first;

    /**
     * 尾节点
     */
    transient Node<E> last;
    
    /**
     * 查询头节点
     */
    public E getFirst() {
        final Node<E> f = first;
        if (f == null)
            throw new NoSuchElementException();
        return f.item;
    }

    /**
     * 查询尾结点
     */
    public E getLast() {
        final Node<E> l = last;
        if (l == null)
            throw new NoSuchElementException();
        return l.item;
    }
    
    /**
     * 移除头节点
     */
    public E removeFirst() {
        final Node<E> f = first;
        if (f == null)
            throw new NoSuchElementException();
        return unlinkFirst(f);
    }

    /**
     * 移除尾节点
     */
    public E removeLast() {
        final Node<E> l = last;
        if (l == null)
            throw new NoSuchElementException();
        return unlinkLast(l);
    }
    
    //.......省略........
}

缓存实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import java.util.HashMap;
import java.util.LinkedList;

/**
 * @desc
 * @date 2021/1/22
 */
public class LRUHashLinkedListCache<K, V> {

    private HashMap<K, V> map;
    private LinkedList<K> list;
    private int capacity;

    public LRUHashLinkedListCache(int capacity) {
        this.map = new HashMap<>(capacity);
        this.list = new LinkedList<>();
        this.capacity = capacity;
    }

    /**
     * 查询
     *
     * @param key
     * @return
     */
    public V get(K key) {
        if (map.containsKey(key)) {
            V value = map.get(key);
            list.remove(key);
            list.addLast(key);
            return value;
        }
        return null;
    }

    /**
     * 新增
     *
     * @param key
     * @param value
     */
    public void put(K key, V value) {
        if (map.containsKey(key)) {
            map.remove(key);
            list.remove(key);
        } else if (map.size() >= capacity) {
            K oldKey = list.removeFirst();
            map.remove(oldKey);
        }
        map.put(key, value);
        list.addLast(key);
    }

}

LFU-最近最少使用

Least Frequently Used：最近最少使用算法（基于使用频次），该算法淘汰最近时期内使用频次最小的数据。该算法为个数据增加个记数据，用于记录被访问的次数，当缓存满时，淘汰次数最小的数据。

实现方案

基于双向链表实现，在链表头插入元素，然后每插入一次计数一次；接着按照次数重新排序链表，如果次数相同的话，按照插入时间排序，然后淘汰链表尾部的数据。

实现示例

节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Node<T> {

    String key;
    T data;
    int times;

    Node<T> preNode;
    Node<T> nextNode;

    public Node(String key, T data) {
        this.key = key;
        this.data = data;
    }
}

双向链表缓存：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
/**
 * @desc
 * @date 2021/1/22
 */
public class LFUDoubleLinkedListCache<T> {

    private static final int DEFAULT_SIZE = 8;

    private Node<T> head;
    private Node<T> tail;

    private int capacity = DEFAULT_SIZE;
    private int size = 0;

    public LFUDoubleLinkedListCache() {
    }

    public LFUDoubleLinkedListCache(int capacity) {
        this.capacity = capacity;
    }

    /**
     * 添加
     *
     * @param node
     */
    public void add(Node<T> node) {
        // 为空
        if (isEmpty()) {
            head = node;
            tail = node;
            size++;
            return;
        }
        // 只有一个
        if (size == 1) {
            if (head.key.equals(node.key)) {
                head.data = node.data;
                head.times++;
            } else if (head.times <= node.times) {
                Node<T> temp = head;
                head = node;
                head.preNode = null;
                head.nextNode = temp;
                temp.preNode = head;
                tail = temp;
                tail.nextNode = null;
            } else {
                head.nextNode = node;
                tail = node;
            }
            size++;
            return;
        }

        Node<T> node1 = get(node.key);
        if (node1 != null) {
            node1.data = node.data;
            return;
        }

        Node<T> target = getTargetNode(node);
        if (target == head) {
            Node<T> temp = head;
            head = node;
            head.preNode = null;
            head.nextNode = temp;
            temp.preNode = head;
        } else if (target == tail) {
            if (tail.times > node.times) {
                Node<T> temp = tail;
                tail = node;
                tail.preNode = temp;
                tail.nextNode = null;
                temp.nextNode = tail;
            } else {
                Node<T> preNode = tail.preNode;
                preNode.nextNode = node;
                node.preNode = preNode;
                node.nextNode = tail;
                tail.preNode = node;
                tail.nextNode = null;
            }
        } else {
            Node<T> preNode = target.preNode;
            Node<T> nextNode = target.nextNode;
            preNode.nextNode = node;
            node.preNode = preNode;
            node.nextNode = nextNode;
            nextNode.preNode = node;
        }

        if (isFull()) {
            Node<T> preNode = tail.preNode;
            tail = preNode;
            tail.nextNode = null;
            tail = preNode;
        } else {
            size++;
        }

    }

    /**
     * 查询并重排序
     *
     * @param key
     * @return
     */
    public Node<T> get(String key) {
        Node<T> temp = head;
        for (; ; ) {
            if (temp == null) {
                return null;
            }
            if (temp.key.equals(key)) {
                temp.times++;
                this.resetSort(temp);
                return temp;
            } else {
                temp = temp.nextNode;

            }
        }
    }

    /**
     * 按使用次数重排序
     *
     * @param node
     */
    private void resetSort(Node<T> node) {
        // 自己就是头,不变
        if (node == head) {
            return;
        }

        // 自己是尾,就近判断
        if (node == tail) {
            // 前一节点仍大于自己
            if (node.preNode.times > node.times) {
                return;
            }
            // 查找替换的目标节点
            Node<T> target = this.getTargetNode(node);
            if (target == head) {
                tail = node.preNode;
                tail.nextNode = null;
                Node<T> temp = head;
                head = node;
                head.preNode = null;
                head.nextNode = temp;
                temp.preNode = head;
            } else {
                tail = node.preNode;
                tail.nextNode = null;
                Node<T> preNode = target.preNode;
                preNode.nextNode = node;
                node.preNode = preNode;
                node.nextNode = target;
                target.preNode = node;
            }
        } else {
            // 非头非尾,就是中间节点

            // 前一节点仍大于自己
            if (node.preNode.times > node.times) {
                return;
            }

            // 查找替换的目标节点
            Node<T> target = this.getTargetNode(node);
            if (target == head) {
                Node<T> temp = head;
                Node<T> preNode = node.preNode;
                Node<T> nextNode = node.nextNode;
                head = node;
                head.preNode = null;
                head.nextNode = temp;
                temp.preNode = head;
                preNode.nextNode = nextNode;
                nextNode.preNode = preNode;
            } else {
                Node<T> preNode = node.preNode;
                Node<T> nextNode = node.nextNode;
                Node<T> targetPre = target.preNode;
                targetPre.nextNode = node;
                node.preNode = targetPre;
                node.nextNode = target;
                target.preNode = node;
                preNode.nextNode = nextNode;
            }

        }
    }

    /**
     * 获取要置换的节点
     *
     * @param node
     * @return
     */
    private Node<T> getTargetNode(Node<T> node) {
        Node<T> temp = head;
        for (; ; ) {
            if (temp == tail) {
                return tail;
            }
            if (temp.times <= node.times) {
                // 返回最近的次数小的节点
                return temp;
            } else {
                temp = temp.nextNode;
            }
        }
    }

    private boolean isEmpty() {
        return size == 0;
    }

    private boolean isFull() {
        return size >= capacity;
    }
}

参考资料

  1. LinkedHashMap 的实现原理
  2. LeetCode 146.LRU 缓存机制
  3. Using Redis as an LRU cache
  4. LRU算法的Java实现
  5. 如何实现LRU缓存淘汰算法?
  6. 数据结构与算法
  7. 缓存淘汰算法–LRU算法
  8. LRU算法四种实现方式介绍
  9. 页面置换算法之Clock算法
  10. clock时钟淘汰算法详解及实现
  11. 内存页置换算法
  12. 内存管理之页面置换算法
  13. 内存管理之页面置换算法
  14. 页面置换算法及其优缺点详解
  15. 内存页面置换算法
  16. 内存页面置换算法
  17. 基于页面置换算法的缓存原理详解
  18. 了解操作系统中的页面置换算法
  19. 缓存淘汰算法–LRU算法

数据结构与算法(五)：FIFO, LRU, LFU 缓存淘汰算法

http://blog.gxitsky.com/2020/11/13/DataStructure-05-cache-LRU-LFU-FIFO/

作者

光星

发布于

2020-11-13

更新于

2022-06-17

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我
×